Google explains the string conversion algorithm 'Burrows-Wheeler conversion' in a movie, and the creator himself appears and explains it.

Burrows-Wheeler Transform (Ep 4, Compressor Head) Google - YouTube
The Burrows-Wheeler transform is not an algorithm that directly compresses data, but rather a reversible data transformation method that rearranges data so that other compression algorithms can process it more efficiently. It is also known as the core technology of the compression tool ' bzip2 ', which is widely used on Linux and other platforms.
Entropy, a general indicator of information content, focuses only on the types of symbols contained in the data and their frequency of occurrence, and does not take into account the 'order' of the symbols.
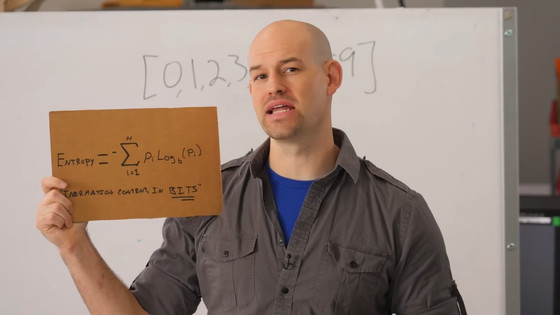
However, compression algorithms use data order and patterns to improve compression rates. The Burrows-Wheeler transform is an algorithm designed to rearrange this 'order' in a way that is advantageous for compression. Specifically, it rearranges the input data (strings of characters) to form 'clusters' where the same characters appear consecutively. This makes the subsequent compression process very efficient. The greatest feature of the Burrows-Wheeler transform is its reversibility, meaning that this complex rearrangement can be completely reversed with just a little additional information: the row index of the original string.
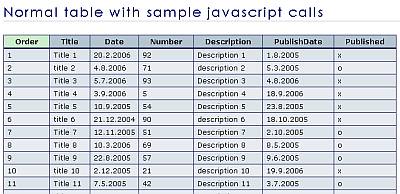
The video explains using the word 'BANANA' as an example.

The original string 'BANANA' is placed on the first line, and from the second line onwards, a circular shift is performed, moving the last character to the beginning one character at a time, for the same number of lines as the length of the string, to create a table.

Sort each row of the created table in lexicographical order, i.e. alphabetical order. The string 'NNBAAA' in the last column of the sorted table is the result of the Burrows-Wheeler transformation.

Additionally, a separate index is maintained that indicates the row number of the original string 'BANANA' in the sorted table. These two pieces of information form the encoding result. The reason why the last column is chosen is because it has the mathematical property that allows the entire original table to be reconstructed.

Decoding uses the string and row index of the last column obtained by encoding. First, arrange the converted string (last column) in one column.

By sorting this column lexicographically, you can restore the first column of the table that was sorted during encoding.

Next, the original converted string (the last column) is concatenated to the front of the restored first column, and each row in this two-column table is then sorted lexicographically again.

Repeating this process for the length of the original string will perfectly restore the sorted table created during encoding.

Finally, the original string 'BANANA' is restored by reading the string in that line using the row index stored during encoding.

The Burrows-Wheeler transform only transforms data and does not compress it by itself. Data clustered by the Burrows-Wheeler transform is typically processed by another technique called the '

In the middle of the movie, the person approaching from behind the commentator is the inventor, Mr. Burrows himself.

According to Burrows, who was introduced as a 'genius,' the Burrows-Wheeler transform was originally conceived by Wheeler, but at the time, computer processing speeds were too slow to be considered a practical algorithm. Later, Burrows, who was a student of Wheeler, realized its importance, devised a fast implementation, and published a paper on it.

Burrows' paper was initially rejected by a data compression conference, but was published as a technical report and gained widespread recognition through a magazine article. It has also been used to efficiently piece together fragmented data in the field of DNA sequencing, achieving significant results in unexpected areas.

Related Posts: