A map coloring game has been released to explain 'zero-knowledge proof' that proves you've found Wally without revealing his location

by
Zero-knowledge proof is a technology that allows a person who wants to prove something to prove that they know something without giving any other knowledge to others other than the fact that they know it. An example of zero-knowledge proof is Where's Wally?, which specifically proves that you found Wally without revealing his location. A game that allows you to intuitively understand various mathematical problems and theorems, including zero-knowledge proof, has been released.
rahulilango.com/coloring/
https://www.rahulilango.com/coloring/
When you access the above URL, a map of the UK and Ireland will be displayed, colored purple. The first question is to 'color this map so that no two adjacent regions are the same color.'
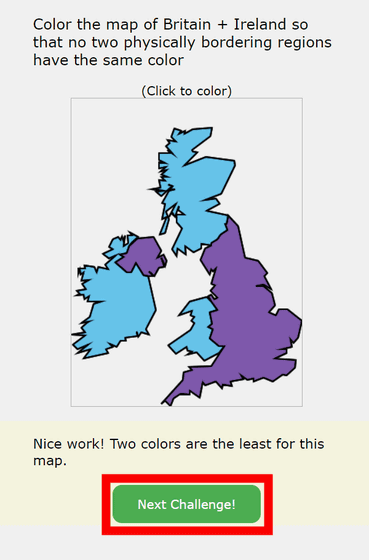
When you click on the map and succeed in color-coding, you will see the message 'This map can be color-coded with two colors.' When you clear the problem, a button called 'Next Challenge!' will appear at the bottom of the screen, so click on it.
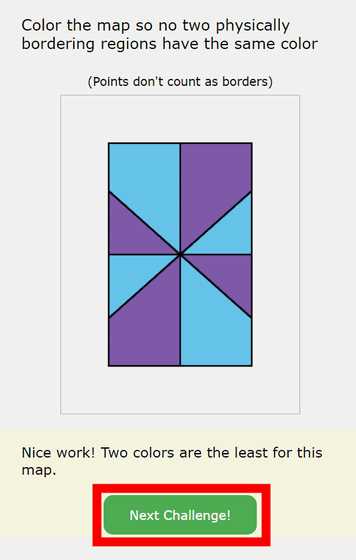
The next problem is as follows. The problem is 'Please color-code two areas so that no two physically adjacent areas are the same color.'

This is also a simple problem with not much difference from the previous problem. Click 'Next Challenge!'
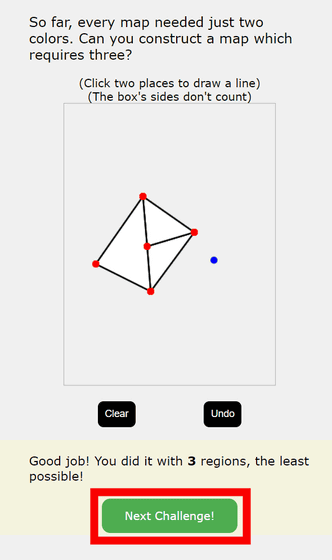
The next question was, 'Can you create a map where three colors are needed to colorize areas so that they are not the same color? ' Move the mouse pointer to the red frame at the bottom of the screen and draw a line to create a map.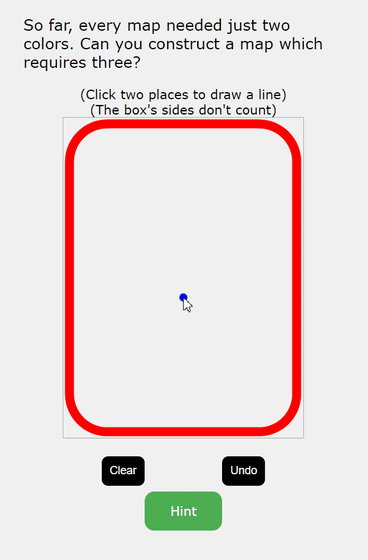
Once you have successfully created the map, click 'Next Challenge!'
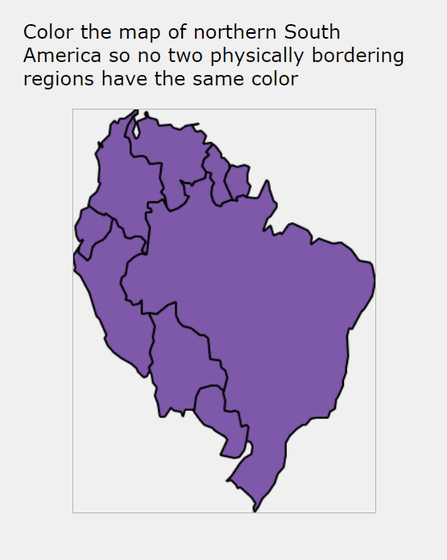
The next question was: 'Color a map of northern South America so that no two physically adjacent areas are the same color.'
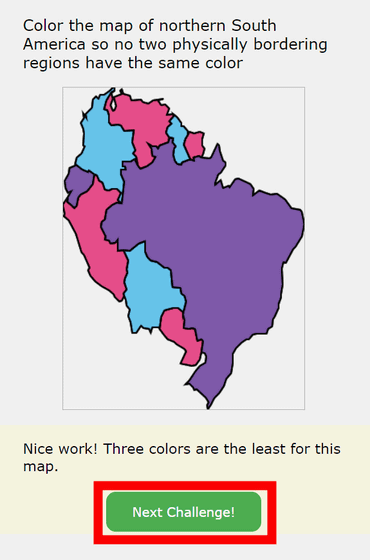
The minimum number of colors required to color the map below was '3'. Click 'Next Challenge!'
The next question is, 'Can you create a map that requires four colors to be colored so that physically adjacent areas are not the same color?' If you can't think of a suitable shape, click 'Hint' to get a hint.
Once you've managed to create the map, click 'Next Challenge!' If you click the hint multiple times, the answer will be displayed, so even if you can't think of the answer, you can proceed to the next problem.

After that, you will be asked several questions using the actual map.
'Color a map of the western United States so that no two physically adjacent areas are the same color.'
'Color a map of South America so that no two physically adjacent areas are the same color.'
If you answered these questions correctly, you were asked the question, 'Can you create a map in which five colors are needed to color-code areas so that no two physically adjacent areas are the same color?' As this is a very difficult question, as shown at the bottom of the screen, there is even a 'Skip' button that says, 'Please skip after trying various things.'
If you skip the problem, the message will say, 'The world's leading mathematicians have puzzled over whether four colors are enough to color any map. This question first arose more than 100 years ago,' and buttons will appear saying '4 is enough!' and '4 is not enough!'.

This was a game to experience
There is an even deeper mystery, so click the green button at the bottom of the screen.

The next question asks whether you can quickly answer the question, 'How many colors would be needed to paint this map so that adjacent areas have different colors?' It asks, 'I claim that three colors are enough, but would you believe me?' If you answer yes, click the button above, if you answer no, click the button below.
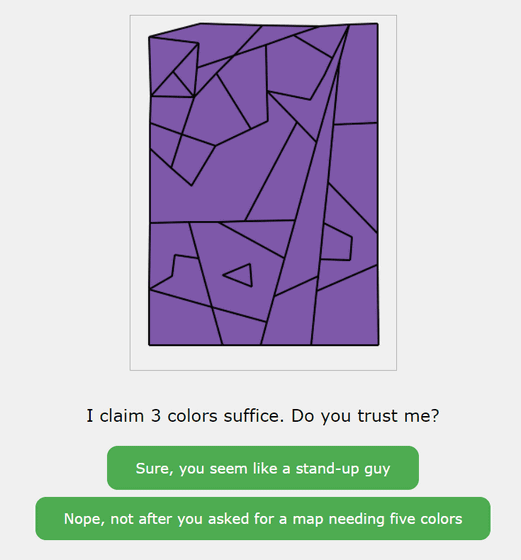
The easiest and most obvious way to prove that you can color the puzzle in three colors is to color the puzzle in three colors. However, doing so would ruin the experience of solving the puzzle. So the question this time is, 'Can you persuade someone without revealing the answer?' If you can't, click the left button, if you can, click the right button.

The answer is yes, and it is possible to show that three colors are enough without providing the answer.
A simple example is as follows:
step 1:
Color each area purple, blue, red, etc., and cover it with a post-it note. Note that we assume that the color cannot be changed after the post-it note is attached.
Step 2:
Peel off any two post-its and make sure they are of different colors.
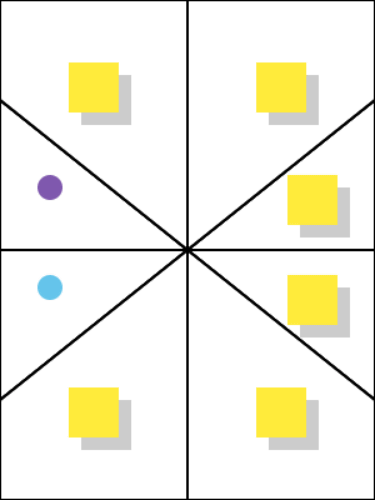
Step 3:
Repeat steps 1 and 2 until the other person is happy, but switch the color underneath the post-it each time you check the colors.
This is called a zero-knowledge proof. Since you only show a part of the map's coloring to your opponent, they don't know the exact coloring method (answer). You also change your answer (coloring) over and over again until your opponent is satisfied, but since the answer changes every time, it is impossible to piece together the colors you see to derive the answer. In addition, by changing your answer over and over again, you can show your opponent that you understand the answer.
The game's creator is Rahul Ilango , a doctoral student in computer science at the Massachusetts Institute of Technology. 'I created this game to interactively illustrate some of my favorite math problems and ideas. My goal is primarily to pique the player's curiosity, not necessarily to explain everything,' he wrote in a Hacker News post .
Related Posts: