How to trap customers who visited in the ``maze that can not escape'' created in a fictitious amusement park for more than 1500 years

The 'giant maze' is an attraction in which a vast space inside a theme park is completely transformed into a maze, and it was booming around 1980 in Japan and was present in various places. A movie explaining how to build such a huge maze with the amusement park management simulation game '
RollerCoaster Tycoon 2-The Impossible Maze-YouTube
When you hear the word 'huge maze,' you might imagine a complex labyrinth-like road, but the 'maze that cannot escape' described here has a simple structure as follows.
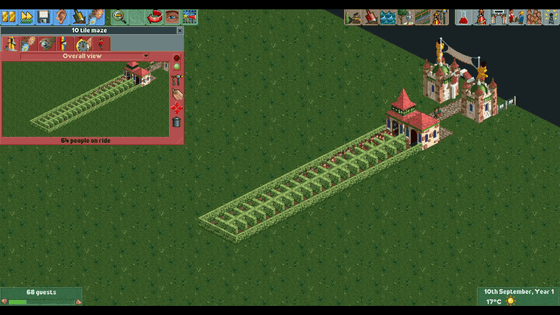
The reason why this simple maze cannot be escaped is due to the character movement algorithm of RollerCoaster Tycoon 2.

In RollerCoaster Tycoon 2, when a character reaches an intersection, the character tries to move randomly by choosing one direction from front, back, left and right. However, even if the character selects 'upper right' as the moving direction in the following cases, it cannot move to the upper right because there is a wall.

If you select a direction that cannot be moved, the character will select the 'direction rotated 90 degrees clockwise' from that direction as the next destination. In this case, I could not move to the upper right, so I try to move to the lower right, but since the lower right is the 'direction I came', the character will not move here either.

Therefore, the character moves to the lower left side in order to select the 'direction rotated 90 degrees clockwise' as the destination. In other words, if you select upper right, lower right, or lower left as in the following cases, the character will eventually move to the lower left.

On the other hand, if the upper left is selected as the destination, it will move to the upper left as it is.

As a result, the probability that the upper left will be selected as the destination is 25%, while the probability that the lower left will be selected is 75%, and the probability that the upper right and lower right will be selected is 0%.

Now, let's consider the case where a character enters a dead end as shown in the figure below. In this case, the character goes back to the intersection after reaching the dead end.

When returning to the intersection, the character will randomly decide the destination from 4 directions as before. However, if you select the upper right, there is a wall, and the lower left is the direction you came in, so it is not selected. If you select the upper right, the result will be the lower right as a result of the clockwise law, and if you select the lower left, the result will be the upper left as a result of the clockwise law.

So if you come out of a dead end, you have a 50% chance of moving to the entrance side and a 50% chance of moving to the exit side.

Therefore, the 'probability that the character turns back to the entrance side at each intersection' is the probability when 'the character moves to the dead end side and moves to the entrance side when exiting the dead end'. When calculated, the probability is 37.5%.

If you create a maze with 38 intersections as shown below, the probability that a character will break through the maze without ever turning back to the entrance side is 0.00000175%.

However, no matter how many times you return to the entrance side, it is possible for the character to break through the maze if you take time. So, I actually created mazes of different lengths as follows and tried to measure the time for the character to break through the maze. The length of each maze is defined by the unit of area in the game, 'tile', and each maze is 5 tiles, 6 tiles, 7 tiles, 8 tiles, 9 tiles, and 10 tiles.

The number of breakthroughs at the time when 2000 has passed in the game time is as follows. There were 14,178 characters who broke through the 5-tile maze...
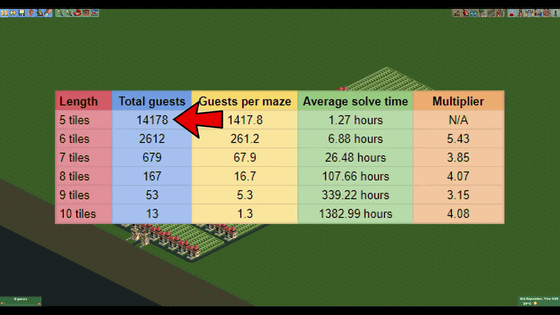
Only 13 characters have broken through the maze of 10 tiles.
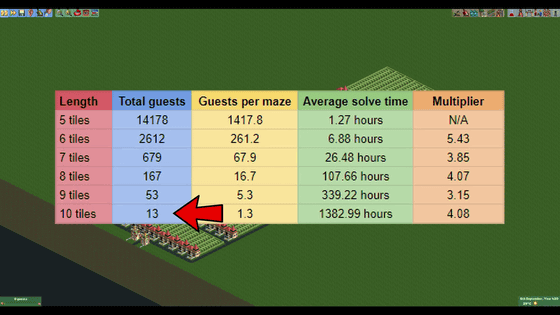
The average breakthrough time for 10 tiles is 1540 in-game time. When converted into actual time, it was 1382.99 hours (approximately 57.6 days). The character who has entered this maze is a calculation that keeps wandering in the maze in 1540.

In addition, if you fill the entire amusement park with similar mazes and build the theoretically largest maze with Roller Coaster Tycoon 2, it looks like this.

If you zoom near the entrance to the amusement park, you can see the hugeness of this maze.

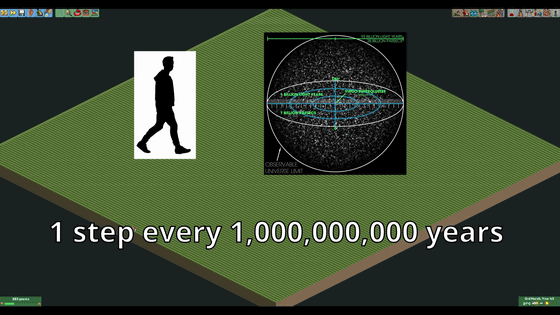
The time it takes to break through this huge maze is 6.6 × 10 19758 in real time. The number 6.6 × 10 19758 is too large to imagine, but if you write without omitting digits in Google Docs, zeros will be arranged over 6 pages.
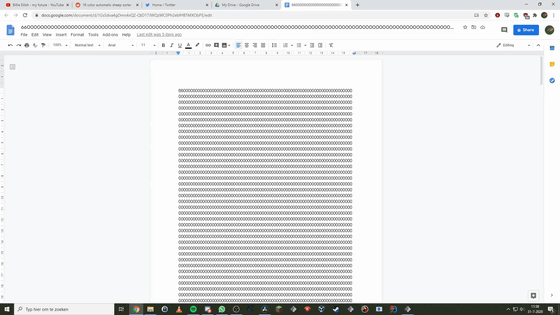
6.6 × 10 19758 is much longer than the time it takes a human to traverse the
In addition, if you introduce a huge MOD '
OpenRCT2 Changed the Maze Pathfinding Algorithm-YouTube
If you introduce OpenRCT2, you can not select the movement such as the direction in which the wall exists or the direction you came, and the destination will be selected with equal probability.

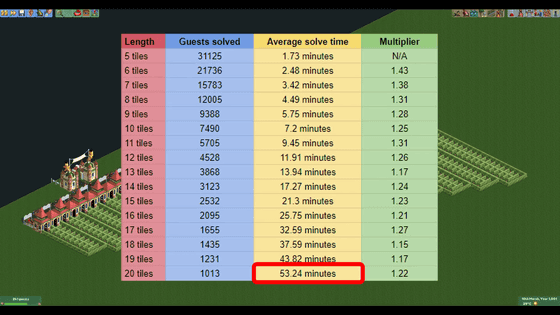
Therefore, even if you create a huge maze for 20 tiles, it will be broken in 53.24 minutes in real time.
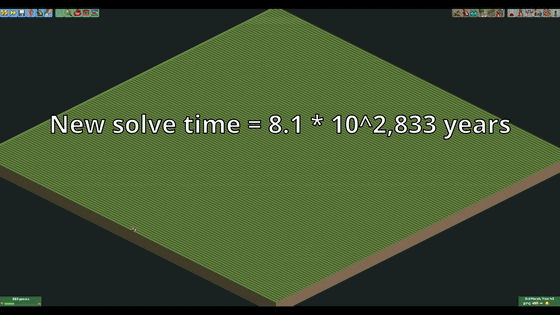
Even if a maze was spread over the entire amusement park, it would have been broken through in just 8.1×10 2833 .
Related Posts:







