When the distance of each planet in the solar system is set to a logarithmic scale, the positional relationship is even

Planets that exist in the solar system have a geometric series relationship with the distance of adjacent planets if they are arranged in order from the sun closest to the sun, the ratio falling within the range of about 1.3 to 3.4. For this reason, John Cook, who runs a consulting firm that explains that the interplanetary distances are expressed on a logarithmic scale, each planet tends to be evenly spaced, explains.

Planets evenly spaced on log scale, including extrasolar
https://www.johndcook.com/blog/2018/04/05/solar-system-on-log-scale/

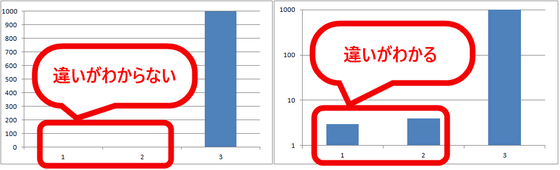
The logarithmic scale is a log scale in the graph. In the normal graph, if you graph three values ​​of "3, 4, 1000", you can not grasp the difference in size between 3 and 4 by looking at only the graph. Therefore, if you use a logarithmic scale on the Y axis and arrange "1, 10, 100, 1000" at equal intervals and graph it, you can see the difference in sizes between 3 and 4 even if there is an outstanding value is.


The following graph shows the distance of the solar system's planet using a logarithmic scale. The vertical axis represents the average distance from the sun (astronomical unit: AU) on a logarithmic scale. Also, the numbers on the horizontal axis show planets, Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, Neptune, andKuiper belt objectsWith PlutoEllisI am wearing numbers in order from the sun. According to this graph, although there is a large gap between No. 4 Mars and No. 5 Jupiter, the other parts are drawn straight lines, which shows that the positional relationship is even.


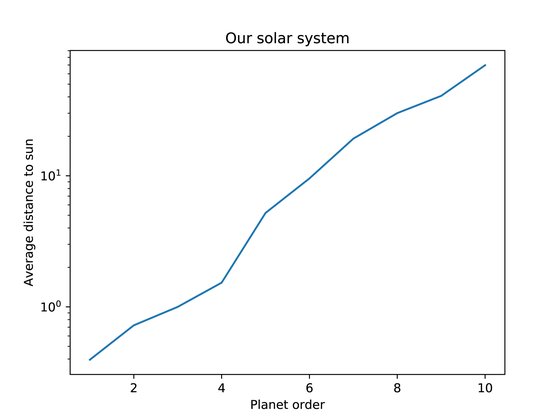
Here, it is the largest celestial body among asteroids existing between Mars and JupiterCeresIs included in the 5th planet, the gap between Mars and Jupiter will be filled and it will have a more even positional relationship than the previous graph.


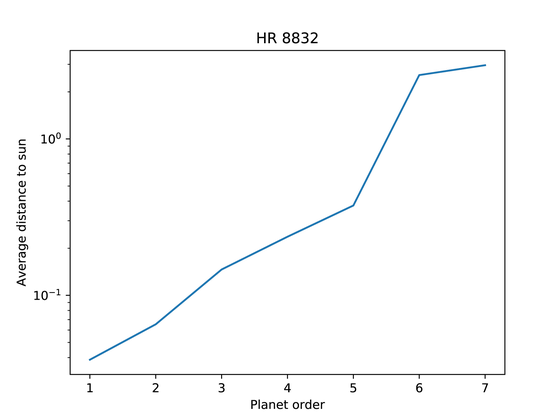
It is said that this law is a coincident product in planetary science as it can not explain the orbit of Neptune, but according to Mr. Cook, "This rule applies to other planetary systems" Other planetary systems are also graphed. The distance from the star to the planet used in the following planetary graph is not the average distance but the distance of the semi-major axis of the elliptical orbit.

Kepler 90It is also known that eight planets existed and were first discovered as a planetary system of the same scale as the solar system. When the distance from the star to each planet is shown on a logarithmic scale, it can be seen that although the positions of the 4th and 5th planets are displaced, they are in a substantially straight shape and are evenly positioned.


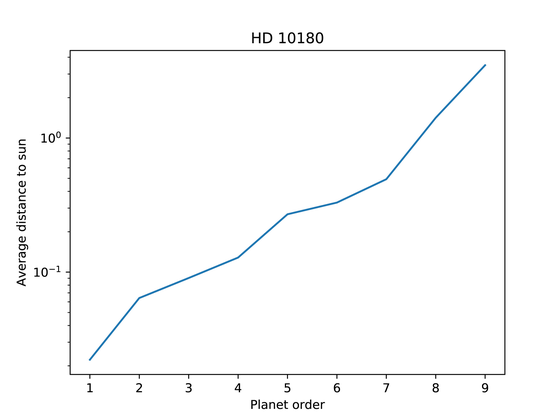
HD 10180There are seven planets and two unidentified planets. The unconfirmed planet in the graph below corresponds to No. 3 and No. 6. Looking at the positional relationship from the stars, the planets of No. 8 and No. 9 are slightly apart, but the planetary system of HD 10180 is almost evenly positioned.


Grise 892Has confirmed the existence of five planets and two unidentified planets. Unknown planets correspond to the fifth and sixth, and when charted, you can see that the position of the sixth planet is greatly displaced. Mr. Cook says, "If the position of the sixth planet turns out to be nearer, it will be in the shape of a straight line."


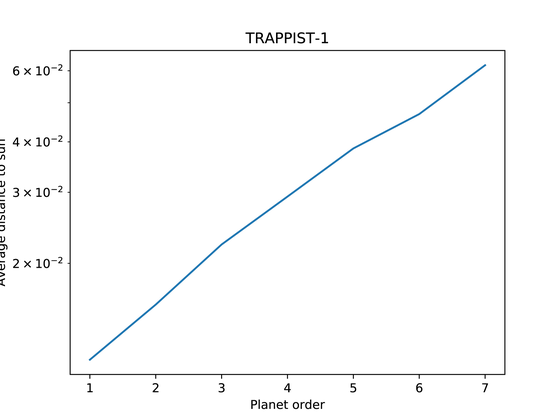
Trapist 1Is characterized by a very short distance between each planet of 0.01 to 0.06 AU. In addition, it can be seen that when the trapist 1 shows the planet's distance on a logarithmic scale, it is more evenly positioned than any other planetary system.


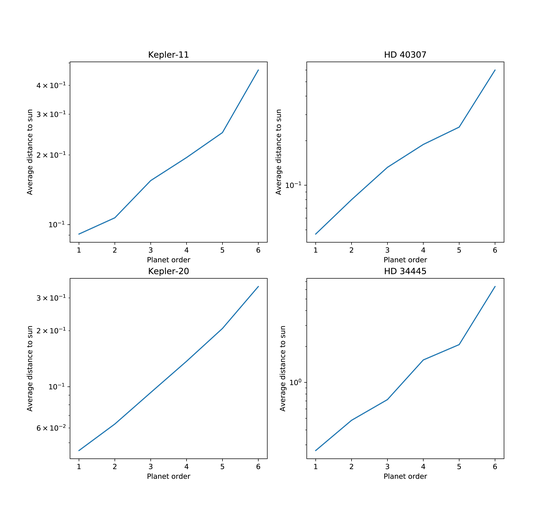
Mr. Cook also has four planetary systems with six planets (Kepler 11,Kepler 20,HD 40307,HD 34445), And they also show that they are in a nearly even positional relationship.


Although it is unknown whether there is a rule or a coincidence in the positional relationship between these planets, it is possible that it will be clarified in a detailed survey in the future.