「数学の美しさを表す」と研究者が示す数学現象5つ

数学は「貝の形」「川の流れ」「銀河の渦」など、自然のいたるところに存在します。子どもの頃から数学を愛し、「美はそれ自体が数学的」だと語るニューサウスウェールズ大学数学統計学科の講師トーマス・ブリッツ氏が、日常存在する「数学と美の結びつきが感じられるもの5つ」を挙げています。

The mystique of mathematics: 5 beautiful math phenomena
https://phys.org/news/2020-05-mystique-mathematics-beautiful-math-phenomena.html

◆1：シンメトリー(対称)

ブリッツ氏は2018年に講演で、「美しいと感じること」のような感情を数学で説明できると語りました。近年の研究から、私たちの脳は「対称的なものを見る」「全体を整理する」「パズルを解く」といった「パターン」を見つけると報酬を得るようになっていることが示されています。そして、予想外なものに出会った時など、パターンから外れる何かを見つけた時にも、脳は報酬を受け取り、喜びやワクワクを得られるとのこと。

例えば、人は対称的な顔を「美しい」と感じますが、ほんの少し対称性を崩す何かがそこにあると、それは魅力として「美しさ」を加えることになります。

音楽にも同様のことが言え、パターンを持つ規則的なサウンドに予想外の要素が合わさると、個性や魅力、深さとして捉えられるようになるとのこと。

「パターンと予期せぬもの」「エレガンスとカオス」「真実と謎」といった多くの数学的概念にも同様のハーモニーが存在すると、ブリッツ氏は述べています。

◆2：フラクタル
フラクタルは部分と全体が自己相似になっているものをいいます。野菜のロマネスコが日常でよく見られるフラクタルの1つで、ロマネスコに近づけば近づくほど、同じ形が繰り返されている様子を見ることができます。

このようなフラクタル構造は雪の結晶や川の流れ、花、樹木のほか、血管など、自然の中のいたるところで見られるとのこと。

自然で見られるフラクタルの層は有限ですが、概念的には、フラクタルの層は無限です。「コンピューターでシミュレーションを行うと、どんなに近づいてもフラクタルの終わりは見えません」とブリッツ氏。

◆3：π
数学で学ぶ「π(パイ)」は簡単に言えば3より少し大きい数字です。円の周囲の長さや面積を計算する時にπが利用されますが、実際のところ、πという概念は「それ以上のもの」だとブリッツ氏は語ります。

「自然に目をやると、至るところにπを見つけることができます。円に結び付くものだけでなく、確率や微積分といった円と全く関係のないものの公式にもπは現れます」とのことで、最も有名な数にも関わらず、πは謎に満ちているそうです。

定義からいうと、πは無限であり、全ての数を知ることはできません。また、2020年時点で小数点以下にパターンも見つかっていません。このため、自分の誕生日や電話番号もπのどこかに存在します。

以下のウェブサイトを使うと、自分の電話番号がπのどのあたりに存在するのかを調べることができます。

Irrational Numbers Search Engine
http://www.subidiom.com/pi/

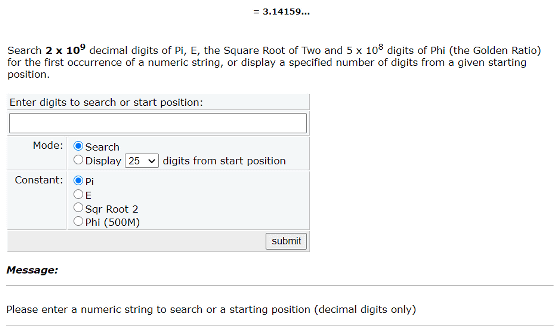
記事作成時点で判明しているπは50兆桁まで。誰もπの正確な値を知らないので、正確な円の面積を求めることはできませんが、その値に近づくことは可能です。世界中の円と結び付くπという数について、ブリッツ氏は「いくつかのπの真実を理解していますが、私たちはπ自体を理解していません。この神秘性が美を作り出しています」と語りました。

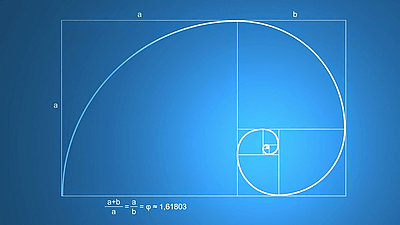
◆4：黄金比
美しさに関係した最も有名な比数が、「物体を最も素晴らしい方法で配置する」といわれる黄金比です。

黄金比は「1.6180339887……」と続く無理数なので、通常は「1.618」と短縮した形で示されます。黄金比を幾何学的・視覚的に表すと、以下のように曲線と長方形で示されます。

「歴史的に、この比率は建築・美術・人の体型において『理想の形』のベンチマークとして扱われてきました。私はこれを神の比率と呼んでいます。レオナルド・ダ・ヴィンチを含む有名な芸術は、この比率を基礎としています」とブリッジ氏。

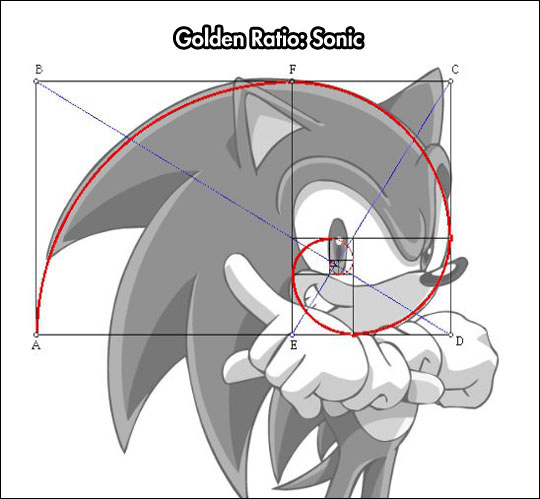
黄金比は今日でもアート・デザイン・写真など幅広い分野で使われており、2014年にはセガのキャラクターソニック・ザ・ヘッジホッグの頭も黄金比でできていたとして話題になりました。

◆5：バナッハ＝タルスキーのパラドックス
バナッハ＝タルスキーのパラドックスは「球体をいくつかのパーツに分割し、それらを組み換えると、元の球と同じ大きさの球を2つ作ることができる」という定理。現実的には手元にあるボールを同じ大きさの2つのボールにすることは不可能ですが、数学的には可能であり、ブリッジ氏は「ある意味、これは魔法です」と語っています。

上記の5つの数学的概念は、数学の美しさの一部に過ぎないとのこと。「たくさんの数学の美しさを知るためには、その背景となる知識が必要です。スポーツ選手が何度も腕立て伏せをするように、基礎的な、退屈極まりない訓練が必要となりますが、その価値はあります。多くの人が数学をもっと楽しめるようになることを願います。ここには隠れた美しさが多くあるのですから」とブリッジ氏は述べました。