「ムーアの法則」に替わる新時代のハードウェア性能進歩を予言する「ネーヴンの法則」とは？

By maxxyustas

量子コンピューターを研究・開発するNASAやGoogleの共同研究施設「量子人工知能研究所(QuAIL)」のハルトマット・ネーヴン所長が「量子コンピューターの処理能力の進化」について予想を発表し、「ムーアの法則」に替わる「ネーヴンの法則」として話題になっています。

Does Neven’s Law Describe Quantum Computing’s Rise? | Quanta Magazine
https://www.quantamagazine.org/does-nevens-law-describe-quantum-computings-rise-20190618/

Neven's Law: why it might be too soon for a Moore's Law for quantum computers
https://theconversation.com/nevens-law-why-it-might-be-too-soon-for-a-moores-law-for-quantum-computers-120706

「量子コンピューター」は一般的な用途ではなく医薬品や材料開発などの特定の科学研究に特化した性能を持ち、それらの分野の研究速度を爆発的に加速させると期待されている新時代のコンピューターです。

量子コンピューターが従来のコンピューターとどう違うのかは以下の記事から読むことができます。

従来のPCの1億倍高速な量子コンピューターはどのような仕組みで動いて物理的限界を突破しているのかがわかるムービー「Quantum Computers Explained」 - GIGAZINE

「ムーアの法則」とは「半導体集積回路のトランジスタ数は約2年ごとに倍になる」という集積回路の進歩に関する予測です。ムーアの法則は発表された1965年から2015年頃まで集積回路の進歩を正確に予言していましたが、通常のコンピューターとは全く異なる原理で動く量子コンピューターは適応外。量子コンピューターは「本当に進歩しているかどうか」も含めて専門家以外には不明瞭でした。そういった背景から、量子コンピューター研究で先駆的な立場のネーヴン所長が量子コンピューターの技術進歩の予測を発表しました。

その発表とは、「量子コンピューターのプロセッサの処理速度は『二重指数関数的に成長』するだろう」というもの。指数関数的とは2(2¹)、4(2²)、8(2³)、16(2⁴)という増加の法則である一方、二重指数関数的とは、以下の画像のような増加の法則で、換算すると4、16、256、65536と増加率がケタ違いに異なります。

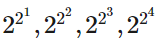
量子コンピューターの近年の発展は、量子コンピューターに使われる回路のエラー率が減少し続けていることに主に起因するもので、その異常なまでの成長率は研究所で行われているプロジェクトの結果から導き出されたものだとネーヴン所長は語っています。

一方で、ネーヴンの法則が成立しているかどうかはまだ未知数です。量子コンピューターはまだまだ発展途上の研究分野であるということや、量子プロセッサが高性能化するにつれて、システム内に発生した電気的ノイズなど小さなエラーの影響が増大するといった懸念があります。

By Pixabay

学術系メディアのThe Conversationは「1965年から2015年頃までの約50年に渡って集積回路の処理能力はほとんどムーアの法則通りに成長し続けたため、ムーアの法則は投資や開発資金などに影響を与え続けました。もしもネーヴンの法則がこの先も成立するのならば、量子コンピューターの先行きを予想する一つの指標になり得ますが、現段階ではわかりません」と記しています。