簡単な「人種隔離シミュレーション」で個人の小さな偏見が社会を歪ませる現実がわかる「多角形のたとえ話」

By woodleywonderworks

ノーベル経済学賞を受賞したゲーム理論学者のトーマス・シェリング氏が提唱した「人種隔離シミュレーション」は、例えば、「白人と黒人が『隣同士で暮らすのに抵抗はない』と考えていても、いつの間にか白人は白人、黒人は黒人で暮らす居住地区ができあがってしまう」という出来事の理由を説明するものです。この人種隔離シミュレーションをわかりやすく能動的に学べるのが「多角形のたとえ話」で、ちょっとしたパズルゲーム感覚で社会を歪ませる「偏見」がどういった効果を生むか分かります。

多角形のたとえ話(Parable of the Polygons) - 多角形社会に関する自分で遊べる記事
http://ncase.me/polygons-ja/

「多角形のたとえ話」では、人間の代わりに三角形と四角形で人種隔離シミュレーションが行われます。

この2種類の形たちは、50％が三角形で、残りの50％が四角形です。すべての形たちはそれぞれが形にちょっとしたこだわりを持っていますが、どれも多様性のある仲間が周りにいてほしいと考えています。

以下のように周りがすべて同じ形だと多様性がありません。なので、ひとりぼっちの三角形は自分の居場所を不満に思うのですが……

三角形と四角形が適度に混じり合った場所に移ると、自分の居場所に満足します。

「多角形のたとえ話」では、このように自分のお隣さんが気に入らず不満げな顔を浮かべる形をドラッグ＆ドロップで動かすことができます。いったん周りの状況に満足すると、その形は再びお隣さんが気に入らなくなるまで動かすことができません。 そして、その他に「自分と同じ形をした仲間が、すぐそばのお隣さんのうち1/3未満しかいなくなった時には、自分もよそを探して引っ越しします。」という簡単なルールが存在します。

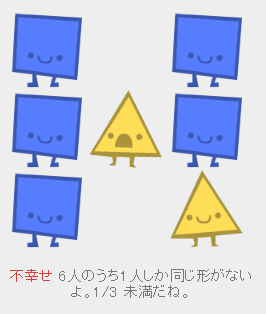
以下の場合、真ん中にいる三角形は自分の周りに同じ形の仲間が1体しかいないので不満、不幸せ。よって、引っ越しせずにはいられません。

以下の配置の場合、すべての形の周りに1/3以上自分と同じ形がいるので、全部の形が自分の居場所に満足します。

そして周りがすべて自分と同じ形の仲間の場合。理想は「他の形が周りにいること」ですが、唯一のルールである「自分と同じ形をした仲間が、すぐそばのお隣さんのうち1/3未満しかいなくなった時には、自分もよそを探して引っ越しします。」は守られているため、形たちが引っ越すことはありません。

つまり、どの多角形も程よく混ざり合った状態を望んでいるわけです。しかし、「周りが自分と違う形だけは嫌だ」という偏見だけが絶対のルールとして存在しています。

次に、以下のような三角形と四角形が多数配置されたボードが登場。このボード上の形がすべて不満を抱かないようにドラッグ＆ドロップで形の配置を変更します。

結果は一様ではありませんが、必ず以下のように三角形は三角形でまとまり、四角形は四角形でまとまる「人種分離状態」に陥ります。これは形たちが悪いことをしたというわけではなく、周りに自分と同じ形がいなくなってしまったため、それぞれがそれぞれと同じ形の近所に引っ越してしまったわけです。三角形が集まる場所では近所に四角形が引っ越してくることを歓迎しますが、そこに来ようとする四角形はもはやひとつもいません。

以下のシミュレーションは、自分の居場所に不満な形は自分でランダムな空いている場所に引っ越していきます。これを繰り返し、全部の形が自分の居場所に満足した時、全体はどれくらいの人種分離状態になるのでしょうか。

シミュレーションをスタートさせるには、「START MOVIN」をクリック。

すると、居場所に不満を持つ形たちが引っ越しを始め、人種分離状態はドンドン上昇。最終的には以下のようにほとんどの形が自分と同じ形と集まってしまいます。

以下のように多様性が保たれた素晴らしい配置でも、たったひとりだけ不満を持つ形がいると……

すべての形を満足させるには、多様性のない近所づきあいで満足せざるを得なくなります。

これは、それぞれの形がほんのちょっとだけ好みに偏りがあるために起きてしまうことで、そういった個人の小さな偏見が、社会全体としての大きな偏りを生み出してしまうということを示しています。それではその個々の偏見が限りなく小さくなった場合やとても偏見が強い場合はどうなるのでしょうか？

以下のシミュレーターは形たちが抱く偏見(自分と同じ形をした仲間が、すぐそばのお隣さんに何％未満になると自分もよそを探して引っ越す)をスライドバーで調整できるシミュレーター。

このスライドバーを動かせば偏見の度合いを変更できます。

例えば、まったく同じ配置で左はもしお隣さんのうち33％未満しか自分と同じ形がいないのであれば引っ越す「偏見度合い33％」で、右がもしお隣さんのうち50％未満しか自分と同じ形がいないのであれば引っ越す「偏見度合い50％」の場合。それぞれどのような配置で形たちは落ち着くことになるでしょうか。

正解は以下の通り。ほんの少し偏見が強いだけで、人種分離状態は一気に高まります。

それでは皆が偏見を持たない場合、形たちの配置はどのように変化するでしょうか。ただし、世界は三角形と四角形の分離状態からはじまります。答えは「誰も動かない」です。

このことから言えるのは、「もし社会に偏見が少しでもあるところから始まったとしたら、偏見をなくすだけでは十分ではない」ということです。それでは、もしもそれぞれの形がほんの少しの多様性を持ちたいと思った場合、どうなるでしょうか。

例えば、「もしお隣さんのうち90％以上が自分と同じ形なのであれば引っ越す」という場合。

それぞれが引っ越しを始めると、以下のようになります。それぞれの形は「自分の周りの90％が自分と同じ形であってほしい」と思っているにもかかわらず、ほんの少しの多様性を持つだけで、形たちの配置は一気に変化します。

これをより多くの形たちでシミュレートするとどうなるのかは、実際にシミュレーターを動かして試してみてください。

それぞれの形がどのような状態を許容できるかは、ほんの少しだけ考え方を変えるだけで大きく変化します。「多角形のたとえ話」は三角形と四角形で人種隔離シミュレーションを行うものですが、これは「三角形と四角形」や「人種差別」に限った話ではありません。社会全体の大きな偏見は個人のちょっとした偏見から生まれることを忘れず、もしもほんの小さな偏見が困った状況を生み出しているなら、それとは逆の「反偏見」を持つことでその状況を打破できるかもしれないことを理解することが大切です。