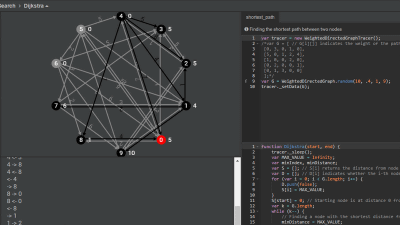
「巡回セールスマン問題」を解くアルゴリズムを可視化したムービー

by Gaël Sacré

いくつもの都市を移動するセールスマンが、すべての都市を最も効率よく(最小の移動コストで)移動できる方法を求める問題を「巡回セールスマン問題」といいますが、その解き方をビジュアル化したムービーがYouTubeで公開されています。

Traveling Salesman Problem Visualization - YouTube


たとえば8つの都市があるとき、これを結ぶルートは5040通りが考えられます。

解法の一つが「欲張り法(Greedy Algorithm)」という、1つの都市から常に最寄りの都市へ移動しようと考える方法。

「最適」ではないものの、最適に近い答えを導き出してくれます。

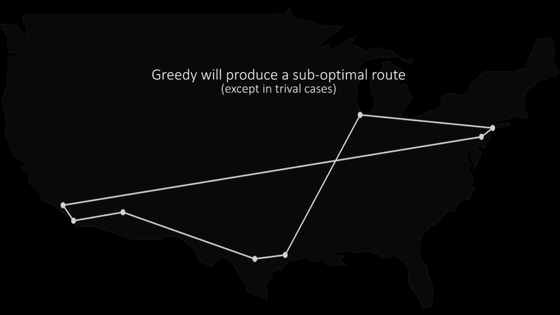
ここで、組み合わせて使うのが「2-opt法」という方法。かなり単純なアルゴリズムで、2辺を繋ぎ直していきます。このとき、ルートに重なりがあると解消して新しいルートを作ります。

「欲張り法」で出た答えを「2-opt法」でもうちょっと最適化したものがコレ。

探索アルゴリズムとしてよく使われるのが「局所探索法」。ここでは、その代表である山登り法のことを指しているようです。

まずはある程度、ランダムにルートを作成。

続いて2点を選んで、よりよいルートがないかを探索し、あれば入れ替えていきます。

この32都市を結ぶルートは1万6592km。局所探索法で作られたルートは「2-opt swap」でこれ以上最適化できないことがありますが……

今回はわずかに最適化することができ、1万4167kmまで減らせました。

しかし、もっと最適なルートはあるはずなのですが、「ローカルな極小値(局所極小値)」にたどりついて探索が終わってしまうことも。

これを避けるべくいくつもの探索アルゴリズムが考えられましたが、そうして出てきたのが局所探索法の1つ、「焼きなまし法(Simulated Annealing)」です。

金属の「焼きなまし」のように、最初は解を出すために与えられる温度のパラメータが大きいため、解は大きく変化しますが、だんだんと温度パラメータは下がっていくため、解の変化が収束していく、という仕組みです。図の左下「Temp」が温度パラメータのこと。最初は大きいので、解の変化も大きいのですが……

最適化が進み、さらに温度が下がってくると解の変化幅が小さくなっていきます。

304の都市だと「2.3×10の624乗」という膨大なルートの組み合わせがあります。山登り法では局所極小値に陥り、大局的な極小値にたどり着けないことがあるのですが、焼きなまし法であれば山登り法よりもよい結果が出せるそうです。