Jan 16, 2020 16:00:00

If a physicist examines how to board an airplane at the fastest speed, the result is counterintuitive

by

Rawpixel

First-class people, children and the elderly prefer to board when flying, but in what order are they most efficient? The problem has not been solved yet. Under such circumstances, a physicist simulated which of `` people who take a long time to board '' or `` people who can ride quickly '' should be countered by intuition, `` People who take a long time to board first It takes less time to complete the boarding process. '

Phys. Rev. E 100, 062313 (2019)-Lorentzian-geometry-based analysis of airplane boarding policies highlights `` slow passengers first '' as better
https://journals.aps.org/pre/abstract/10.1103/PhysRevE.100.062313

Letting slower passengers board airplane first really is faster, study finds | Ars Technica
https://arstechnica.com/science/2020/01/letting-slower-passengers-board-airplane-first-really-is-faster-study-finds/

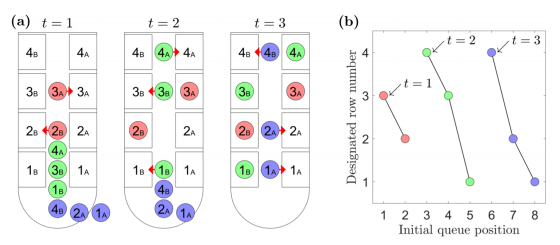
A number of researchers have begun working on the question of 'how to make flying faster and smoother?' In 2011, astrophysicist Jason Stephen considered the problem of flying a plane the same as traveling salesman , `` taking passengers from the back of the plane is most efficient. '' I made the expectation.

However, when Stephan actually calculated, this method was found to be the least efficient. The `` best way '' that Stefan derived by computer simulation is `` to go to the seat in order from the back to the front, and from the window side to the aisle side alternately on the right and left sides across the central aisle '' It was so.

Actually

conducting an experiment with Boeing 757, the Stefan method can put passengers in the seat at twice the speed of 'the method of putting on from behind', 20 to 30% faster than random boarding did. 'The more you parallel the boarding process, the faster you go,' Stefan said.

And in a recent study published in December 2019, Stefan took a different approach to modeling the boarding process using Lorentz geometry, the mathematical basis of Einstein's general relativity. Adopted. As a result, contrary to intuition, it was shown that boarding an airplane was 'efficient when giving priority to passengers who take a long time to board'. 'This is similar to the relationship between two events in space-time, where one passenger is blocking the other, the two passengers are separated in time, and spatially separated if they can be seated at the same time. 'Said Stephen.

Specifically, it was shown that getting first the passengers who take longer is 28% more efficient than getting the first passengers who don't have much time first. The results did not change, considering the number of time-consuming passengers, the time it takes to get seated, and the density of passengers in the aisle.

The figure below shows the time taken to complete boarding when the red graph puts 'fast passenger first' and the blue graph puts 'slow passenger first'. It is smoother to put 'faster passenger first' halfway, but ultimately 'slower passenger first' takes less time to complete boarding.

Mr. Stephen explains this phenomenon as `` the same as trying to pack stones and sand in a jar '', `` If you put sand first, there will be no room for large stones, If you put it in first, you can put sand in the gaps around it. '

Of course, the situation is different between simulation and actual boarding, and in reality it is necessary to consider the existence of first class and the number of people who direct the boarding. On the other hand, such studies are also thought to be very helpful for airlines in developing boarding policies.