黄金比が生む美にインスパイアされて考えられた「ハリスの螺旋」

数を扱う数学は機械的で無機質なものと捉えられることも多いのですが、実は意外なほど美的な要素を持っていることがあり、昔から数には数学的な美があったり、音楽と数学は関連があるものと考えられていたことも。アメリカ・アーカンソー大学のエドムンド・ハリス助教は黄金比が描く図形にヒントを得て、これまでに存在しなかったという新しい図形を描くことに成功したそうです。

The golden ratio has spawned a beautiful new curve: the Harriss spiral | Alex Bellos | Science | The Guardian
http://www.theguardian.com/science/alexs-adventures-in-numberland/2015/jan/13/golden-ratio-beautiful-new-curve-harriss-spiral

新たな図形を考案したエドムンド・ハリス氏は、アメリカ・アーカンソー大学の芸術科学数学部で助教を務める人物。数字が生みだすアート作品を生みだしている人物でもあります。

そのハリス氏が新たに考案した図形がこちら。一部分と全体が相似するフラクタルな図形となっており、その曲線は黄金比にもとづく黄金螺旋をベースにアレンジされたものとなっています。

◆黄金螺旋とは？
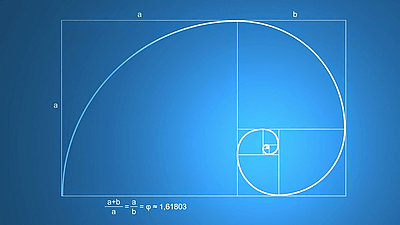
図形のベースになったのは、縦と横の比率が1.618の黄金比となっている黄金長方形です。黄金長方形は、その中に正方形(白い部分)を描くと、残りの部分(青)が再び黄金長方形になるという性質を持っています。

上記のようにして新たに生まれた黄金長方形をさらに同じ方法で分割すると、また新たな黄金長方形が現れます。このようにして、黄金長方形は無限に小さく分割して行くことが可能です。

次に、それぞれの正方形の中に、2つの対角を通る四分円(しぶんえん)を描き、円弧をつなげていくと徐々に小さく(大きく)なる渦巻き状の螺旋(らせん)が描かれます。このようにして描かれた螺旋が「黄金螺旋」で、黄金律を説明する際によく用いられる有名な図形ともなっています。(ただし、正しい黄金螺旋は曲率が滑らかに変化する等角螺旋であり、この図が示すものは厳密には黄金螺旋にはなっていないのですが、ここでは省略します)

◆黄金螺旋をベースにアレンジ
黄金比は古代ギリシアの時代から用いられてきたものといわれており、有名なパルテノン神殿やピラミッドにもその影響を見いだすことができるとされています。ハリス氏はそんな黄金比をもとにする黄金長方形と黄金螺旋に対し、新たな試みを持ち込みます。

その試みについてハリス氏は「正方形を描く代わりに、長方形を描いてみたんだ」と語ります。以下の図はその分割方法を示しているのですが、ここでハリス氏はまず2つの相似の長方形(青とオレンジ)を描き、その結果として正方形(白)が残る分割方法を見つけました。ここで描かれた長方形は、黄金比(1.618)とは異なる「1.325」という縦横比を持っています。

このようにして描かれた長方形を、さらに同じ比率で分割して行きます。

さらにどんどん分割。この時点で、図形はフラクタルの様相を示してきています。

このぐらいまで分割したら、そろそろ螺旋を描くタイミング。上記の黄金螺旋を描いた時は、正方形の2つの対角を通る四分円を描いたことを思い出しておいて下さい。

ここでハリス氏は、白い正方形で対角ではなく2つの隣り合う角を通る四分円を描くという新たな試みを持ち込みます。一目見ただけだと黄金螺旋と同じような螺旋が描かれているわけですが、まだ図形内には円弧の描かれていない白い正方形が残されているのが重要なポイント。

同様の方法で全ての正方形に円弧を描くと、次々と「枝分かれ」する小さな螺旋がいくつも現れました。黄金螺旋は1つの中心から広がる1つの等角円が描かれましたが、ハリス氏が描く螺旋は同じ形状をした円弧が次々と現れるフラクタル図形となっています。

最後に一番大きな円弧を消すと、螺旋で構成された一つの図形ができあがりました。これこそがハリス氏が作成した「ハリスの螺旋」と呼ぶべき図形です。

この図形を目にした時、ハリス氏はその美しさに大喜びだったと言います。ハリス氏の最初の狙いはイスラム美術やクリムトの作品に見られるような枝分かれ螺旋を描くことだったそうなのですが、それがじつに数学的なプロセスを経て生みだされたことに驚きを感じたそうです。この図形が生まれたことに関してハリス氏は「誰も見たことがないものを作ること自体はそれほど難しいことではありません。しかし本当に難しいのは、数学的でありつつ誰も見たことがない新しいものを作り上げることです」と語っています。

事実、ハリス氏はこの手法で描かれた例があるのではと心配していたようで、「数学上の発見と数学美術の難しい点は、たとえその手法が全く新しいものだったとしても、それが『以前に誰も試したことがない』ということを保証するものではないということです」と語っています。

「ハリスの螺旋」を生みだした長方形の比率は先述の通り「1.325」だったのですが、これは数学で言うところのプラスチック数というものであり、これまでにこの数字を用いて図形が描かれたことはなかったことが判明。晴れて「ハリスの螺旋」は正真正銘のハリス氏考案のものであることがわかりました。ハリスの螺旋はTシャツに描かれたり……

トランプや、ハリス氏の車のナンバープレートホルダーに描かれたりしています。

◆それ以外の比率によって描かれる図形
ハリス氏がさらに取り組んでいるのが、ハリス氏が「Proportion Systems(比率系)」と呼ぶ多くの広がりを持つ図形分割法に持ち込むことだとのこと。ある図形を繰り返し分割しても相似する図形が現れ続けるという図形の比率を求めるもののようですが、その図形の原則は「正方形と、相似の長方形にのみ分割される長方形」というもの。この原則を満たす図形は以下の比率を持つ3つの図形のみに限定されることがわかっています。左上の1.41421(＝√2)の比率を持つ図形は、「A4用紙」などの「A列」の紙と同じ比率を持つものになっています。右上の図形はいわゆる黄金律を持つ図形で、下の図形は正方形が2つ並ぶシンプルなものとなっています。

さらに、同様の原則を用いて今度は3つに分割する場合、その形状は16通りが可能になります。そのうち、正方形が1つと2つの相似する長方形に分割できる組み合わせは以下の6通り。

また、相似する長方形を持ち、長方形および正方形が右側に一列に並ぶ組み合わせは以下の6通りのみ。左下の組み合わせは、上記の「ハリスの螺旋」を生みだした組み合わせになっています。

そして、3つの図形が横一列に並ぶものは以下の4通りのみとなっています。

数学に明るい人であれば、上記のイラストで示されている数字が代数的数であることに気付くかもしれません。ハリス氏はこの幾何学的アプローチによってさらにその理解が進むものと考えているそうです。

このようにして描かれた螺旋図は、ハリスの螺旋の他にも以下のようなものが生まれています。なかなか多くのパターンを生みだすのは難しいようですが、数学には不思議な芸術の力が備わっていることを感じさせる例となっていると言えそうです。

ハリス氏のページでは、数学の理論を基にして描かれた数々の図形が掲載されており、興味のある人には興味深いものといえそうです。

Edmund Harriss